Monday, April 10, 2006
Just Another Math Monday
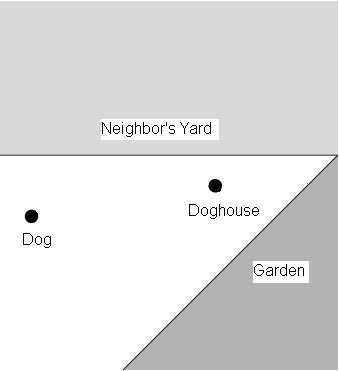Consider a lazy, naughty, nosy dog who wants to peer over the fence into the neighbor's yard, dig up the flowers in the garden, and then go to his doghouse to take a nap, all the while taking the absolute shortest route possible. What path should he take?Please only post answers that you have solved using mathematic principles, not ones that you've figured out how to google the right five word combination to get an answer from the internet. (Although I would be curious as to what approach you took to arrive at that, so please feel free to email me...)
The first to post a correct answer as a comment shall be awarded one Dunkin Donut at a time and place to be determined by mutual agreement. I'll give the magic google words at the close of the contest next Monday morning.
Links to this post
Comments:
He should run and leap up onto the doghouse, that way he can see into the neighbors yard. Then he just needs to walk a line perpendicular to the edge of the garden there and back.>
Yes. I suspected that would disqualify my answer. Is his correct path described by a line perpendicular to the garden intersecting the doghouse and continuing on to the fence, from that point a straight line back to his starting point?>
Ted -
Let's assume that the tasks are to be completed in the order presented. However, if you reverse the order of the garden and the fence, the same principle for determining the shortest route would apply. (It makes no sense to have the doghouse be anywhere but last...)
Jason -
Since that would mean walking a portion of the same path twice, your solution is not the shortest possible route.>
Let's assume that the tasks are to be completed in the order presented. However, if you reverse the order of the garden and the fence, the same principle for determining the shortest route would apply. (It makes no sense to have the doghouse be anywhere but last...)
Jason -
Since that would mean walking a portion of the same path twice, your solution is not the shortest possible route.>
How about if the dog goes to the spot where the garden and yard join (at the point). Then all he needs to do is walk to that point, peer into the neighbor's yard, then in the same spot dig up the flowers, then walk back over to his dog house and go to sleep.
-Christy>
-Christy>
Jason,
I agree with you. Although your answer is not correct, I did not give you an adequate reason as to why. I will tell you that the shortest distance between two points is still a straight line.>
I agree with you. Although your answer is not correct, I did not give you an adequate reason as to why. I will tell you that the shortest distance between two points is still a straight line.>
Simply "unfold" the puzzle so that the entire journey can be described by a straight line. First rotate the lower half of the puzzle around the line describing the fence. then rotate the doghouse around to the other side of the line describing the edge of the garden. Then draw a straight line from the start to the finish. Mark the points of intersection, fold the puzzle back up, and there is the solution.
-J>
-J>
Jason -
If I understand what you're saying, it's almost completely accurate. Here's how I would describe it (see image):
(1) pick a random point anywhere along the fence. (F')
(2) find the image (D') of the dog (D) in the neighbor's yard by reflecting it about the fence. (D')
(A) would you agree that the distance between the D and F' is equal to the distance between D' and F'?
(3) repeat this process for a point along the edge of the garden (G') and the image (H') of the doghouse.
(4) now draw a straight line connecting D' and H', noting the point along the fence (F) and garden (G).
(B) would you agree that the shortest path for the dog is defined by these two points, based on the fact that for any other points F' and G', the path from D' to H' is not a straight line?
Congratulations Jason! Another donut for you. How's Sunday work?>
Post a Comment
If I understand what you're saying, it's almost completely accurate. Here's how I would describe it (see image):
(1) pick a random point anywhere along the fence. (F')
(2) find the image (D') of the dog (D) in the neighbor's yard by reflecting it about the fence. (D')
(A) would you agree that the distance between the D and F' is equal to the distance between D' and F'?
(3) repeat this process for a point along the edge of the garden (G') and the image (H') of the doghouse.
(4) now draw a straight line connecting D' and H', noting the point along the fence (F) and garden (G).
(B) would you agree that the shortest path for the dog is defined by these two points, based on the fact that for any other points F' and G', the path from D' to H' is not a straight line?
Congratulations Jason! Another donut for you. How's Sunday work?>
Links to this post:
|
| 
|
|  |
